Spectral analysis (1)

Introduction

Newton used glass separted the white sunlight into red, orange, yellow, green, blue, indigo and violet single colors. The light spectrum analysis can help scientists to interpret the world. For example, we can detect the elements of our solar system as well as far stars in the universe. The spectrum analysis is also a field in mathmatjics. In the graph thoery field, Laplacian matrix is used to represented a graph. We can obtian features from the undirected graph below (wikipedia).

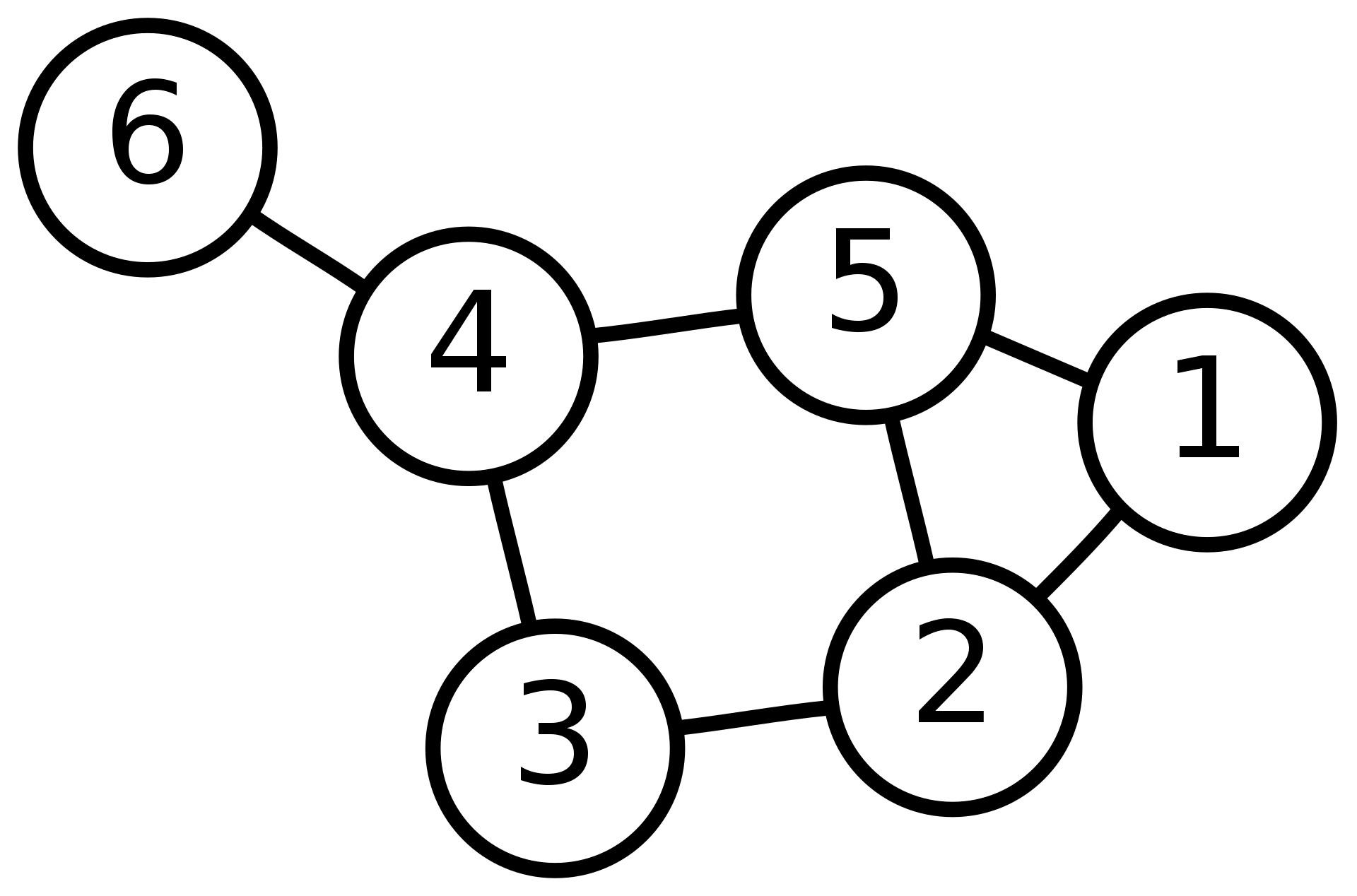
For example, we can check the degree of each vertex, which forms our Degree matrix \(D\) such that: \[\begin{equation} D = \begin{pmatrix} 2 & 0 & 0 & 0 & 0 & 0\\ 0 & 3 & 0 & 0 & 0 & 0\\ 0 & 0 & 2 & 0 & 0 & 0\\ 0 & 0 & 0 & 3 & 0 &0\\ 0 & 0 & 0 & 0 & 3 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 \end{pmatrix} \end{equation}\]

By checking the connection between all pairs nodes, we can create a Adjacency matrix:

\[\begin{equation} A = \begin{pmatrix} 0 & 1 & 0 & 0 & 1 & 0\\ 1 & 0 & 1 & 0 & 1 & 0\\ 0 & 1 & 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0 & 1 &1\\ 1 & 1 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0 \end{pmatrix} \end{equation}\]

graph laplacian

The graph Laplacian \(L\) extracts all useful information from a graph which is: \[\begin{equation} L=D-A =\begin{pmatrix} 2 & -1 & 0 & 0 & -1 & 0\\ -1 & 3 & -1 & 0 & -1 & 0\\ 0 & -1 & 2 & -1 & 0 & 0\\ 0 & 0 & -1 & 3 & -1 & -1\\ -1 & -1 & 0 & -1 & 3 & 0\\ 0 & 0 & 0 & -1 & 0 & 1 \end{pmatrix} \end{equation}\]

In fact, the graph Laplaican matrix is symmetric and also positive semidefinite (PSD), which means if we perform eigenvalue decomposition, the eigen values are all real and nonnegative. We can normlize the graph Laplaican by left multiplying the \(D^{-1}\) which will give rise to all \(1\)s of the diagnal entries of the matrix, namely: \[\begin{equation} \text{norm}({L}) = D^{-1}L = \begin{pmatrix}1 & -0.50 & 0 & 0 & -0.50 & 0\\ -0.33 & 1 & -0.33 & 0 & -0.33 & 0\\ 0 & -0.50 & 1 & -0.50 & 0 & 0\\ 0 & 0 & -0.33 & 1 & -0.33 &-0.33\\ -0.33 & -0.33 & 0 & -0.33 & 1 & 0\\ 0 & 0 & 0 & -1 & 0 & 1 \end{pmatrix} \end{equation}\] This matrix is called transition matrix. However, the matrix would not keep the symmetric and the PSD property after the normalization. We will come back to discuss the spectral for the normalized graph Laplacian.

Weighted graph

In practice, graph are usually weighted. The weight between vertices can be euclidean distance or other measures. The figure blow shows the weights of the graph. Here we apply gussian kernel to the euclidean distances between vertices such that: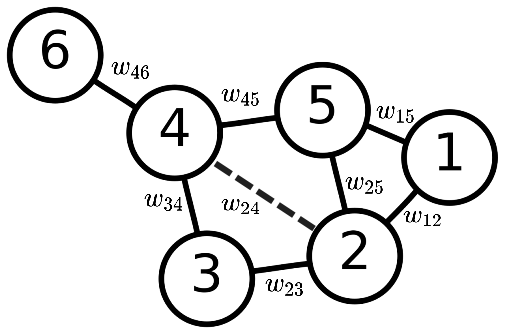

\[\begin{equation} w_{ij} =\exp (-r_{ij}^2/\sigma) = \exp \big(\frac{-\|x_i - x_j\|^2}{\sigma_i\sigma_j}\big) \end{equation}\] where \(r_{ij}\) is the euclidean distance between vetex \(i\) and \(j\), and \(sigma\) controls the bandwidth. We call the matrix \(W=(w_{ij})\) gaussian affinity matrix such that: \[\begin{equation} \begin{pmatrix} 0 & w_{12} & w_{13} & w_{14} & w_{15}& w_{16}\\ w_{21} & 0 & w_{23} & w_{24} & w_{25}& w_{26}\\ w_{31} & w_{32} & 0 & w_{34} & w_{35}& w_{36}\\ w_{41} & w_{42} & w_{43} & 0 & w_{45}& w_{46}\\ w_{51} & w_{52} & w_{53} & w_{54} & 0& w_{56}\\ w_{61} & w_{62} & w_{63} & w_{64} & w_{65}& 0 \end{pmatrix} \end{equation}\] The guassian kernel would enlarge the distance between too far vertices. Similar to unweighted matrix, we can also construct graph Laplaican matrix using the gaussian affinity matrix. First, we need find the weighted degree based on \(W\) such that: \[\begin{equation} d_{ii} = \sum_j{w_{ij}} \end{equation}\] With the diagnal degree matrix and affinity matrix, we now can have the weighted laplacian that: \[\begin{equation} L = D - W \end{equation}\] Likewise, we next give the normalized form of Laplacian such that: \[\begin{equation} \text{norm}{(L)}= D^{-1}L = I - D^{-1}W \end{equation}\] To facilitate the eigenvalue decomposition, we need apply trick to the asymmetric matrix \(D^{-1}L\). Since the eigenvectors of \(D^{-1}L\) and \(D^{-1}W\) are the same, we apply some trick to \(P = D^{-1}W\) to simplify the problem. Lets construct \(P'\) such that: \[\begin{equation} P' = D^{1/2} P D^{-1/2} = D^{-1/2}WD^{-1/2} \end{equation}\] It obvious \(P'\) is symmetric due to the symmetrisation of \(W\). We can perform eigenvalue decomposition on \(P'\) such that: \[\begin{equation} P' = S\Lambda S^\top \end{equation}\] Where S stores the eigenvectors of \(P'\) and the diagonals of \(\Lambda\) records the eigenvalues of \(P'\). We can also get the decompostion to \(P\) such that: \[\begin{equation} P = D^{-1/2}S\Lambda S^\top D^{1/2} \end{equation}\] Let \(Q=D^{-1/2}\), then \(Q^{-1}=S^{\top}D^{1/2}\). We therefore find the right and left eigenvector of \(P\) such that: \[\begin{equation} \psi = D^{-1/2} S \qquad \phi = S^{\top}D^{1/2} \end{equation}\] In fact, columns of \(\psi\) stores the spectral of the graph which also call diffusion map dimensions.