Spectral analysis (2)

发表于

Diffussion map

Eigenvalue decomposition of weighted graph laplacian is used to obtain diffusion map. The asymmetric matrix or transition matrix \(P=D^{-1}W\). The decomposition is: \[\begin{equation} P = D^{-1/2}S\Lambda S^\top D^{1/2} \end{equation}\] In fact, the random walk on the graph would give rise to the transition graph such that: \[\begin{equation} p^{t+1}= p^t D^{-1}W = p^t P \end{equation}\] where \(p\) is a initial state of the graph (vertices weight). That is, after a certain step of random walk on the graph, we would reach a steady state when any more random walk would not change the weight. Let \(Q=D^{-1/2}S\), then \(Q^{-1}=S^{\top} D^{1/2}\), we can derive \(P = Q\Lambda Q^{-1}\). The random walk above mentioned can then be represent: \[\begin{equation} \begin{aligned} P^t &= Q\Lambda Q^{-1}Q\Lambda Q^{-1}\cdots Q\Lambda Q^{-1} &= Q\Lambda^t Q \end{aligned} \end{equation}\] Since \(\Lambda\) is diagnoal, the random walk on a graph can be easily cacluted by using the eigenvalue decomposition outcome. The column of \(Q\) is the diffusion map dimensions.

Diffusion map example

To understand diffusion map, we here introduce an example data and run diffusion map on it. The data is a single cell fibroblasts to neuron data with 392 cells. We first download the data from NCBI and loaded the data to memory:

1
2
3
4
5
6
7
import requests
url = 'https://www.ncbi.nlm.nih.gov/geo/download/?acc=GSE67310&format=file&file=GSE67310%5FiN%5Fdata%5Flog2FPKM%5Fannotated.txt.gz'
r = requests.get(url, allow_redirects=True)
open('GSE67310.txt.gz', 'wb').write(r.content)
data = pd.read_csv('GSE67310.txt.gz', sep='\t', index_col=0)
data = data.loc[data['assignment'] !='Fibroblast']
group = data['assignment']

From the code as we can see that, we extract the cell types from the data and stores it into the variable group. The rest part of the data is the normalized gene expression count matrix.

To do the pre-processing, we first get the log-normalized count matrix \(X\) and revert it to the counts and apply log geomatric scaling to the count matrix as the pre-processing then store it to matrix \(Y\). 

1
2
3
X = np.array(data.iloc[:, 5:]).T
X = np.power(2, X[np.apply_along_axis(np.var, 1, X)>0, :]) - 1
Y = np.log(gscale(X+0.5)).T
The geomatric scaling implementation is: 
1
2
3
4
5
6
7
8
9
def gscale(X:np.ndarray) -> np.ndarray:
    assert(X.all()>=0)
    div_ = np.divide(X.T, np.apply_along_axis(lambda x:np.exp(np.mean(np.log(x))), 1,
    X)).T
    scale_ = np.apply_along_axis(np.median,0, div_)
    sc = StandardScaler(with_mean=False)
    sc.fit(X)
    sc.scale_ = scale_
    return sc.transform(X)
After the pre-processing, we we next run PCA to perform dimensionality reduction and use which to calculate euclidean distances between cells, and then run diffusion map.

1
2
3
pc = run_pca(Y, 100)
R = distance_matrix(pc, pc)
d = diffusionMaps(R,7)

We first take a look at the PCA figure which shows the first 2 PCs of the dataset. PCA is a linear methods which cannot reflect cell fate differentation process. 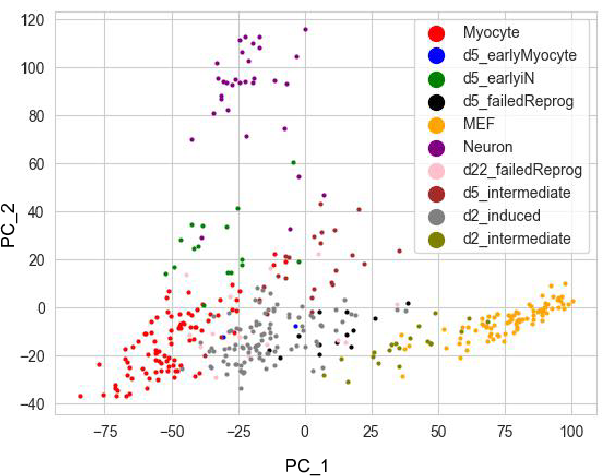Since the diffusion map applied the Gaussian kernal during the distances calculation, it usually a better way to capture the cell differentation events. Here we show diffusion dimension 1,2 and 1,3. It's clear that 1,2 captures the cell differentation from fibroblasts to neuron, and 1,3 captures the differentiation from firoblasts to myocytes.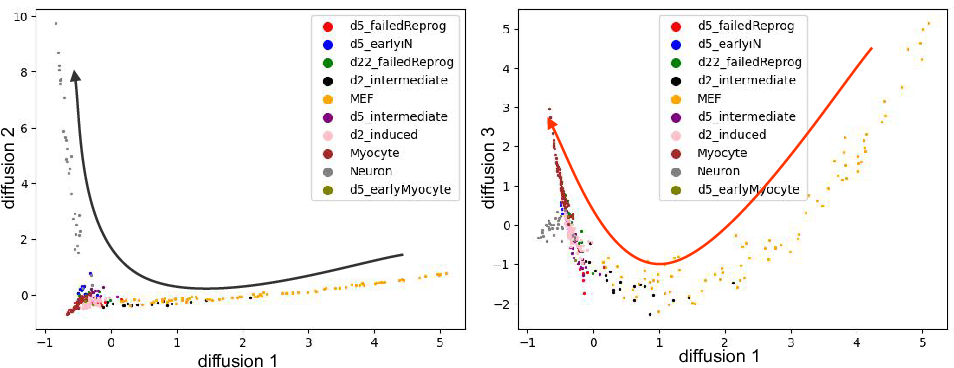

We can change the bandwidth from 7 to 100, which use the 100th neareast neighbor as bandwidth instead of 7th. The following shows the diffusion map that bandwidth=100.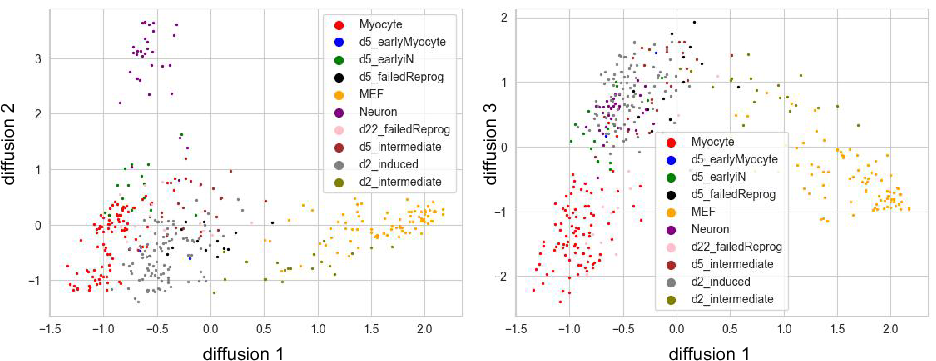

pseudo time by random walk

The eigenvalue decomposition of graph laplacian can also be used to infer the pseudo time simulating the pseudo time of cell differentation events. We here set top \(m\) cells \(1/m\) of the progenitor cells (MEF) and set other cell 0 as the initial state. Next, we perform random walk to get new pesudotime \(u\) such that: \[\begin{equation} u = [\frac{1}{m}, \frac{1}{m}, \cdots, 0, \cdots 0](D^{-1}W)^t \end{equation}\] By testing different number of random walk steps we can check the new pseudo time \(u\). Here we show time step equals to 1, 10, 100 and 200. From the figure we can notice that after certain step, the pseudo time will not change anymore. That means the random walk reaches the steady state.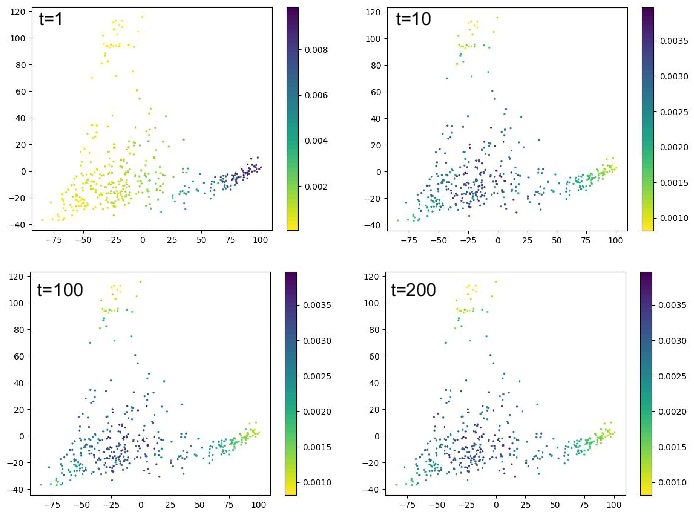

To test when can we reach the steady state, I use the graph we mentioned in my last post Spectral analysis (1):

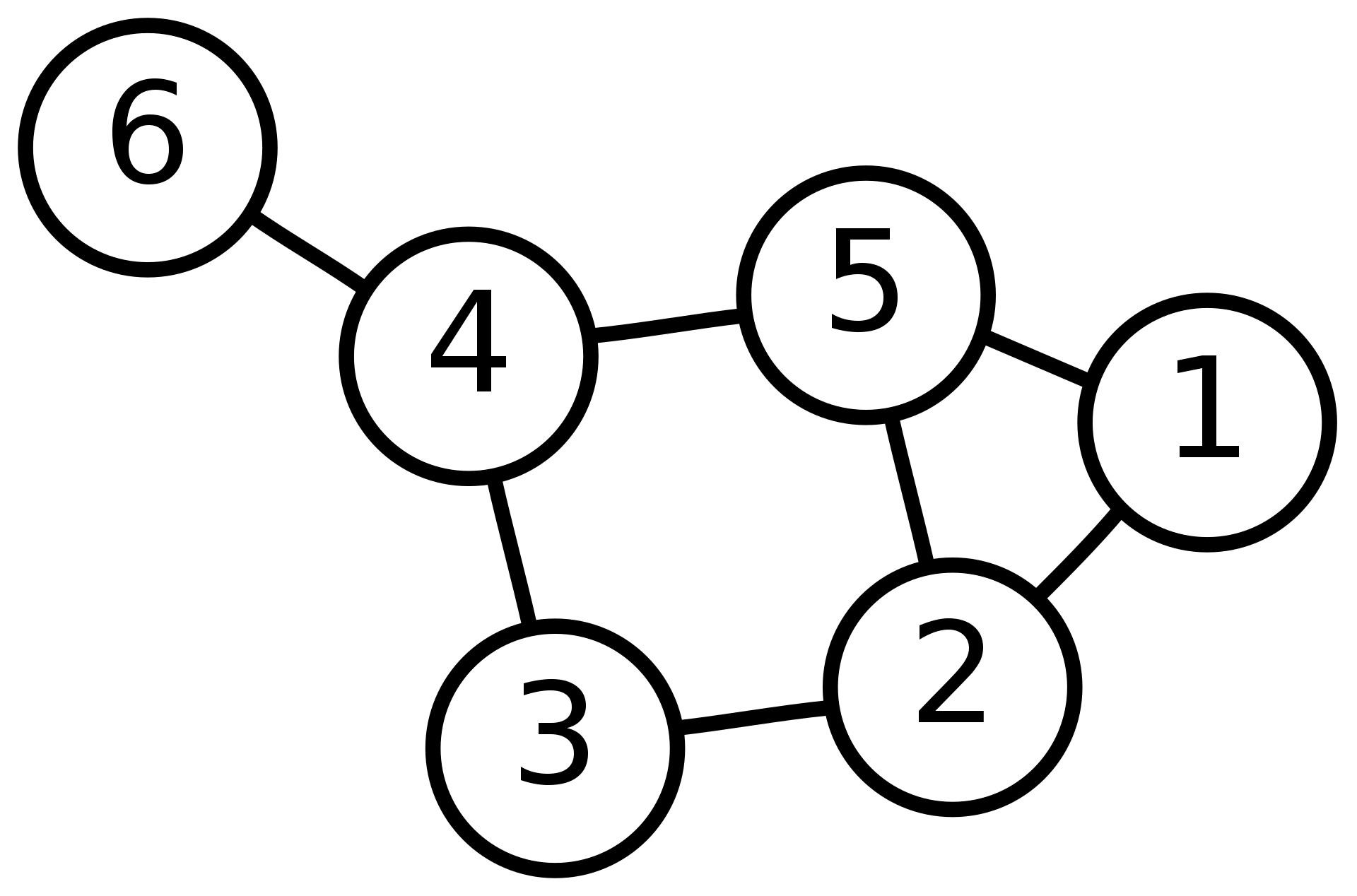
Here we random generate two initial states (\(v_1\), \(v_2\)) to do the random walk such that: \[\begin{equation} \begin{aligned} v_1 &= [0.15,0.41,0.54,0.9,0.62,0.93,0.1,0.46,0.01,0.88]\\ v_2 &= [0.89,0.93,0.07,0.41,0.52,0.88,0.43,0.09,0.1,0.2] \end{aligned} \end{equation}\]

From the the figure below we can see that \(v_1\) reaches the steady state in 30 steps whereas \(v_2\) reaches steady state in 100 steps. In total, all these two initial state will reach the steady state that would not change any longer.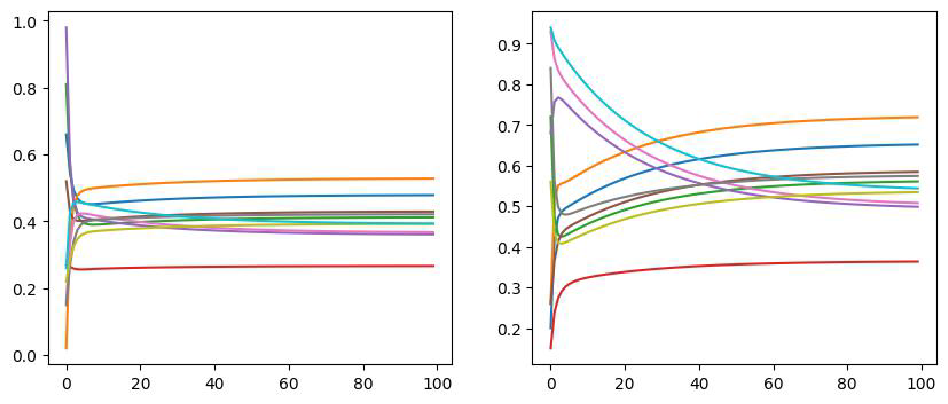

spectral clustering

The eigenvectors of graph Laplacian can also be used to do the clustering. From the figure we can find clear cut using the 1st, 2nd and the 3rd diffusion dimensions. In practice, we can use kmeans, DBSCAN, leiden, louvain algorithm to perform clustering using the diffusion dimensions.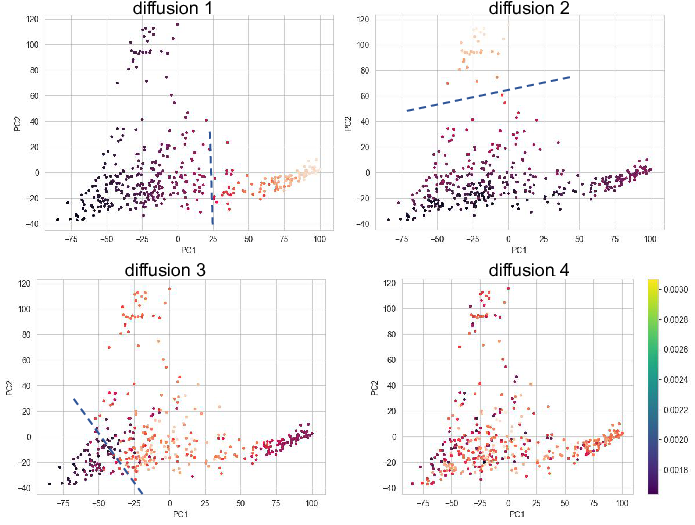

Appendix

PCA function
1
2
3
4
5
6
7
8
9
def run_pca(mtx, n_components=2, random_state=2022):
    dm = None
        if scipy.sparse.issparse(mtx):
        clf = TruncatedSVD(n_components, random_state=random_state)
        dm = clf.fit_transform(mtx)
    else:
        pca = PCA(n_components=n_components, random_state=random_state)
        dm = pca.fit_transform(mtx)
        return dm
Affinity matrix function
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def affinity(R, k=7, sigma=None, log=False):
    """
    Gaussian affinity matrix constructor
    W = exp(-r_{ij}^2/sigma)
    """
    def top_k(lst, k=1):
        assert(len(lst) >k)
        return np.partition(lst, k)[k]

    R = np.array(R)
    if not sigma:
        s = [top_k(R[:, i], k=k) for i in range(R.shape[1])]
        S = np.sqrt(np.outer(s, s))
    else:
        S = sigma
        logW = -np.power(np.divide(R, S), 2)
    if log:
        return logW
    return np.exp(logW)
Diffusion map function
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def diffusionMaps(R,k=7,sigma=None):
    """
    Diffusion map(Coifman, 2005)
    https://en.wikipedia.org/wiki/Diffusion_map
    ----------
    dic:
        psi: right eigvector of P = D^{-1/2} * evec
        phi: left eigvector of P = D^{1/2} * evec
        eig: eigenvalues
    """
    k=k-1 ## k is R version minus 1 for the index
    logW = affinity(R,k,sigma,log=True)
    rs = np.exp([logsumexp(logW[i,:]) for i in range(logW.shape[0])]) ## dii=\sum_j
    w_{i,j}
    D = np.diag(np.sqrt(rs))
    ## D^{1/2}
    Dinv = np.diag(1/np.sqrt(rs)) ##D^{-1/2}
    Ms = Dinv @ np.exp(logW) @ Dinv ## D^{-1/2} W D^{-1/2}
    e = np.linalg.eigh(Ms) ## eigen decomposition of P'
    evalue= e[0][::-1]
    evec = np.flip(e[1], axis=1)
    s = np.sum(np.sqrt(rs) * evec[:,0]) # scaling
    # Phi is orthonormal under the weighted inner product
    #0:Psi, 1:Phi, 2:eig
    dic = {'psi':s * Dinv@evec, 'phi': (1/s)*D@evec, "eig": evalue}
    return dic